Blog

Numero triangolare: numero rappresentabile in forma di triangolo; presa una quantità di elementi pari al numero in esame, è possibile disporre gli elementi in modo da formare un triangolo equilatero, isoscele o rettangolo.

Ad es. : presi 3 punti  ● ● ●  è possibile disporli sul  foglio in modo tale da formare un triangolo

●                                 ●        

● ●      opppure     ●       ●         

in modo analogo per 6 punti

●                                 ●        

● ●                        ●       ●                            

● ● ●                  ●     ●      ●

I primi 10 numeri triangolari:  1, 3, 6, 10, 15, 21, 28, 36, 45, 55, …

(1, dal punto di vista figurativo, può essere immaginato come un triangolo di dimensioni talmente ridotte che si vede un solo punto).

N-esimo numero triangolare  Tn = somma dei primi N numeri naturali.

Ad es.:

T₁ = somma del primo numero naturale = 1

T₂ = somma dei primi due numeri naturali (1+2) = 3

T₃ = somma dei primi tre numeri naturali (1+2+3) = 6

Quindi la successione dei numeri triangolari  è:

• T₁ = 1
• Tn = Tn-1 + n  (n = 2, 3, 4, …)

In forma più sintetica:

• Tn = ∑ k   (per k da 1 a n)

Formula di Gauss:

• Tn = n*(n+1)/2

Alcune proprietà dei numeri triangolari:

1. Differenza tra 2 numeri triangolari vicini:  dalla (2) si ha  Tn – Tn-1 = n

3 – 1    =  2

6 – 3    =  3

10 – 6  =  4

15 – 10 = 5

21 – 15 = 6

28 – 21 = 7

36 – 28 = 8

45 – 36 = 9

55 – 45 = 10

• Ogni numero può essere ottenuto come somma di al massimo 3 numeri triangolari

Ad es. 

            91 = 55 + 36

            14 = 10 + 3 + 1

• Somma di 2 numeri triangolari vicini: è un numero quadrato

1 + 3      =        4          =          2²

3 + 6      =        9          =          3²

6 + 10    =        16        =          4²

10 + 15 =        25        =          5²

15 + 21 =        36        =          6²

21 + 28 =        49        =          7²

28 + 36 =        64        =          8²

36 + 45 =        81        =          9²

• Per stabilire se n è un numero triangolare si deve calcolare l’espressione

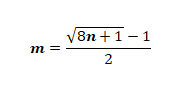
Se m è un intero allora n sarà l’m-esimo numero triangolare, infatti,  sostituendo n con

                        Tm = m*(m+1)/2    il termine sotto radice diventa:

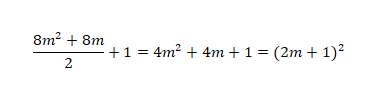
quindi:

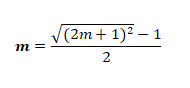
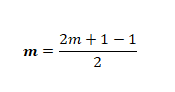
                                    m = m

Esercizi sui numeri triangolari

1. Stampare i primi N numeri triangolari.
2. Dato un numero, verificare se è un numero triangolare.
3. Calcolare l’N-esimo numero triangolare.
4. Calcolare il primo numero triangolare maggiore di N.
5. Calcolare il primo numero triangolare minore di N.

Esercizio 1

Stampare i primi N numeri triangolari.

Variabili

Input	Comodo	Output
n: intera	k: intera	somma: intera (è il numero triangolare di posizione k)

n: valore, fornito dall’utente, che indica quanti numeri triangolari si devono stampare.

k: variabile che permette di generare tutti i numeri naturali a partire da 1 fino a n.

somma: numero triangolare di posizione k, infatti, tenendo presente le

• T₁ = 1
• Tn = Tn-1 + n  (n = 2, 3, 4, …)

i vari numeri triangolari vengono generati sommando al vecchio numero triangolare Tn-1 (somma) il valore attuale di n (k).

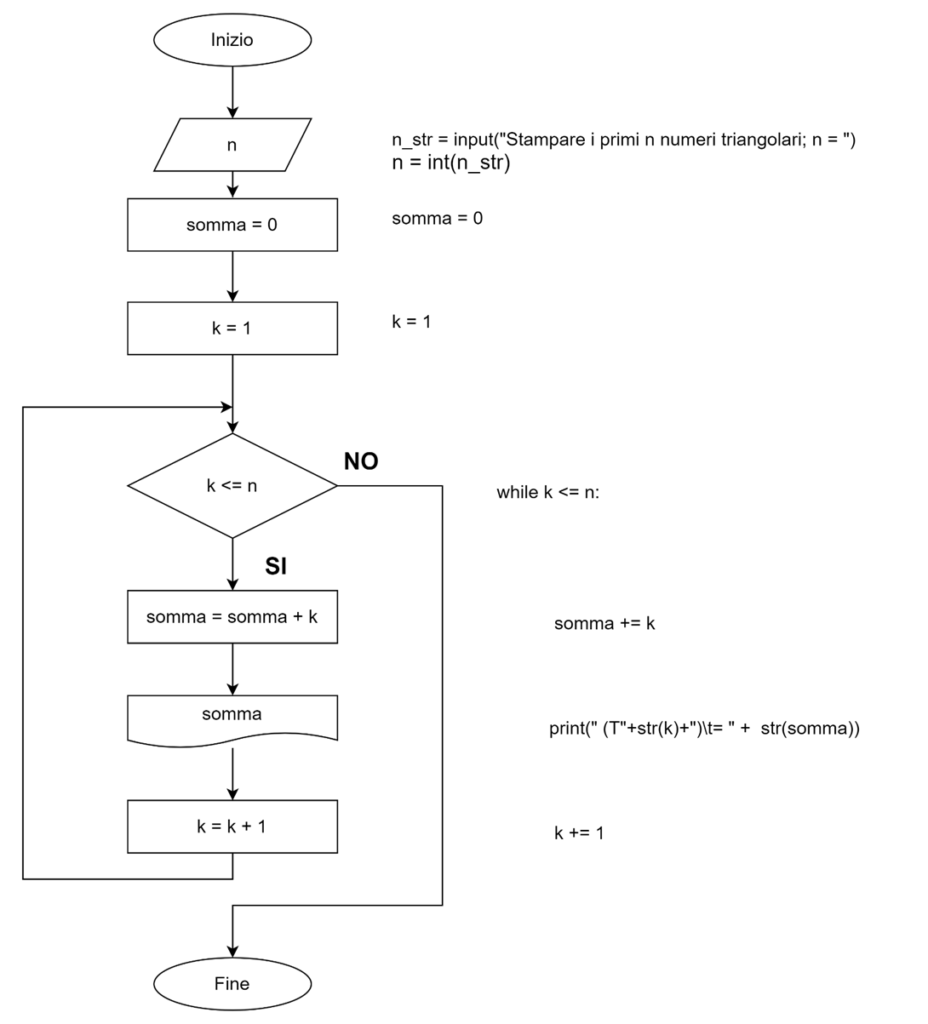
#NumeriTriangolari_es_001

#rispetto al diagramma a blocchi, viene stampato anche il triangolo di “*”  costruito man mano che

#si generano i vari numeri triangolari. 

#—- Main ———-

n_str = input(“Stampare i primi n numeri triangolari; n = “)

n = int(n_str)

somma = 0

k = 1

triangolo = “pos.(i)\tT(i)\n”                                       #prima riga del triangolo di “*”

while k <= n:

    somma += k

    print(” (T”+str(k)+”)\t= ” +  str(somma))

    j = 0                                                                       #riga k-esima del triangolo di “*”

    triangolo += str(k)+ “\t”+ str(somma)+ “\t”

    while j < k:

        triangolo += “*”

        j += 1

    triangolo += “\n”

    k += 1

print()

print (triangolo)

print (“\nFINE”)

Esercizio 2

Dato un numero n, verificare se è un numero triangolare.

Variabili

Input	Comodo	Output
n: intera	k: intera	somma: intera (è il numero triangolare di posizione k)

n: valore, fornito dall’utente: numero da controllare.

k: variabile che permette di generare tutti i numeri naturali a partire da 1 fino a n.

somma: numero triangolare di posizione k, infatti, tenendo presente le

• T₁ = 1
• Tn = Tn-1 + n  (n = 2, 3, 4, …)

i vari numeri triangolari vengono generati sommando al vecchio numero triangolare Tn-1 (somma) il valore attuale di n (k). La generazione dei numeri triangolari ha termine quando somma (ultimo numero triangolare generato) >=  n; in tal caso se somma = n allora si può concludere che n è un numero triangolare.

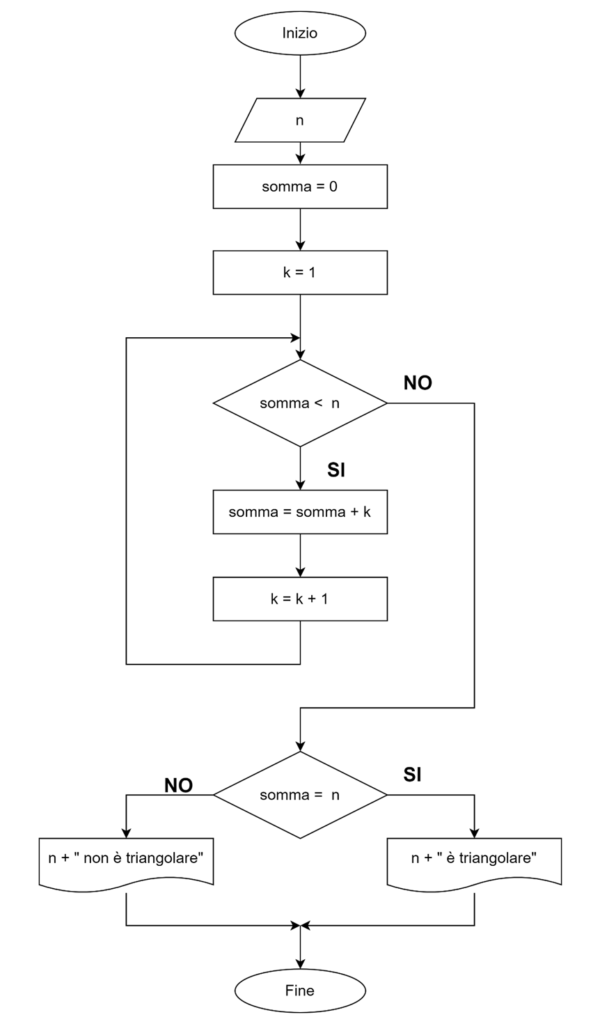
# NumeriTriangolari _002 – codifica Python

#—- Main ———-

n_str = input(“Verificare se è triangolare il numero: “)

n = int(n_str)

somma = 0

k = 1

while somma < n:

    somma += k

    k += 1

print()

if (somma == n):

    print(“Il numero ” + n_str + ” è il numero triangolare di posizione: ” + str(k-1))

else:

    print(“Il numero ” + n_str + ” non è un numero triangolare”)

print (“\nFINE”)

Esercizio 2a

Dato un numero n, verificare se è un numero triangolare utilizzando la seguente formula:

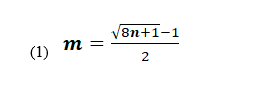
se n è un numero triangolare m deve essere un intero.

Perché m possa essere intero:

• il termine sotto radice (radicando)  b = 8n + 1 deve essere un quadrato perfetto cioè b = c² con c numero naturale  > 1 
• il numeratore della (1) deve essere un numero pari.

Proprietà dei quadrati perfetti: un numero intero è un quadrato perfetto quando, scomposto in fattori primi, gli esponenti dei fattori primi sono tutti pari.

Variabili

Input	Comodo	Output
n: intera	k: intera	messaggio
	radicando: intera
	radice: intera
	etriangolare: boolean

            radicando è un quadrato perfetto? Si utilizza la funzione quadratoperfetto per verificarlo.

            radice -1 (numeratore della (1) ) è pari? si utilizza l’operatore modulo (%)

(a%b resto della divisione intera tra a e b)

• (radice -1) % 2 = 0  allora è pari
• (radice -1) % 2 <> 0  allora è dispari

Variabili funzione quadratoperfetto

Input	Comodo	Output
q: intera	k: intera	eqp: boolean
	esponente: intera

            Funzione quadratoperfetto(q): il valore passato come parametro (q)

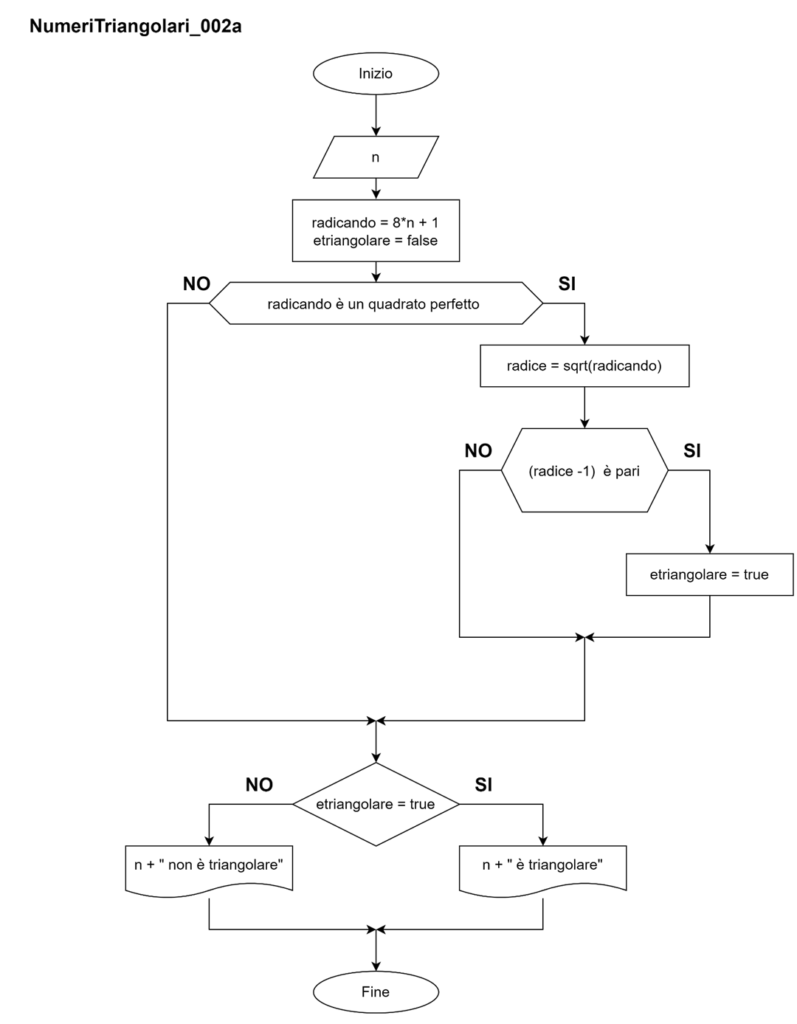
Funzione quadratoperfetto

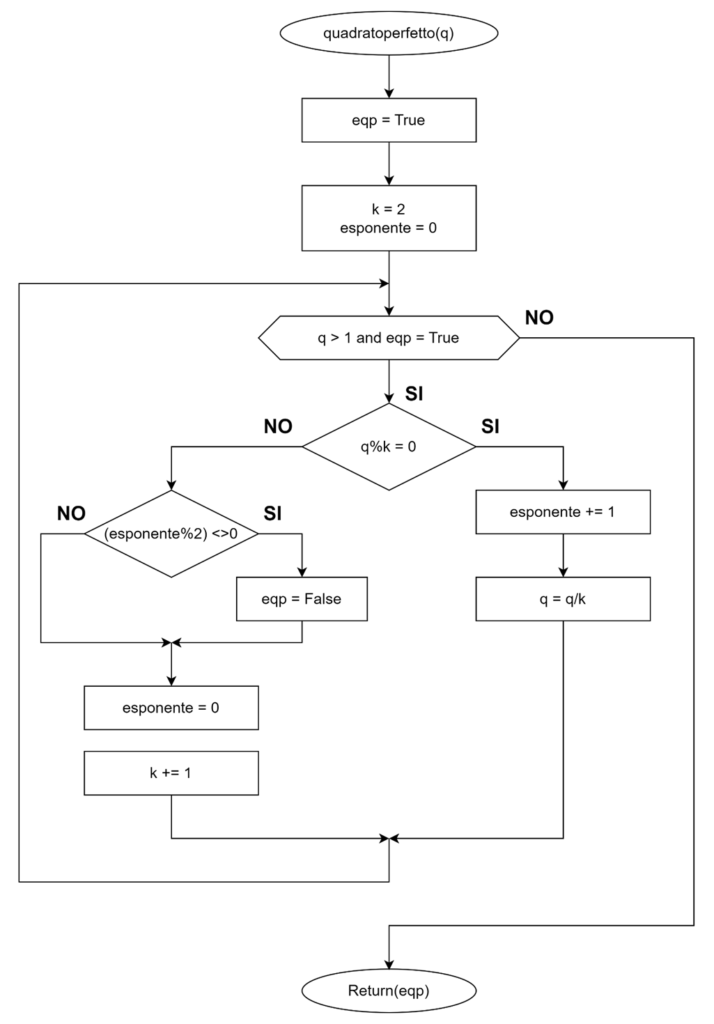
Programma Python

 

#NumeriTriangolari_es_002a

#verifica se n è triangolare utilizzando la formula

#m = (sqrt(8n+1)-1)/2

import math

def quadratoperfetto(q):

    eqp = False                #è (q)uadrato (p)erfetto

    k = 2

    esponente = 0

    epari = True

    while (q > 1 and epari):

        if (q%k == 0):

            esponente += 1

            q /= k

        else:

            if (esponente % 2 != 0):

                epari  = False

            esponente = 0

            k = k +1

    if epari:

        eqp = True

    return (eqp)   

#—- Main ———-

n_str = input(“valore = “)

n = int(n_str)

etriangolare = False

radicando = 8*n + 1

if quadratoperfetto(radicando):

    radice = math.sqrt(radicando)

    if (((radice – 1) % 2) == 0 ):

        etriangolare = True

        m = int((radice -1) / 2)

if (etriangolare):

    print (n_str,” è triangolare  di posizione”, str(m))

else:

    print (n_str,” non è triangolare “)

print()

print (“\nFINE”)